প্রত্যেক ত্রিভুজের ছয়টি অংশ আছে: তিনটি বাহু এবং তিনটি কোণ। ত্রিভুজের এই ছয়টি অংশের কয়েকটি অপর একটি ত্রিভুজের অনুরূপ অংশের সমান হলে দুটি ত্রিভুজ সর্বসম হতে পারে। সুতরাং কেবল ঐ অংশগুলো দেওয়া থাকলে ত্রিভুজটির আকার নির্দিষ্ট হয় এবং ত্রিভুজটি আঁকা যায়। নিচের উপাত্তগুলো জানা থাকলে একটি নির্দিষ্ট ত্রিভুজ সহজেই আঁকা যায়:

(১) তিনটি বাহু
(২) দুটি বাহু ও এদের অন্তর্ভুক্ত কোণ
(৩) একটি বাহু ও এর সংলগ্ন দুটি কোণ
(৪) দুটি কোণ ও এর একটির বিপরীত বাহু
(৫) দুটি বাহু ও এর একটির বিপরীত কোণ
(৬) সমকোণী ত্রিভুজের অতিভুজ ও অপর একটি বাহু অথবা কোণ।

সম্পাদ্য ১

কোনো ত্রিভুজের তিনটি বাহু দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

মনে করি, একটি ত্রিভুজের তিনটি বাহু a, b, c দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কন:
(১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC কেটে নিই।

(২) B ও C বিন্দুকে কেন্দ্র করে যথাক্রমে c এবং b এর সমান ব্যাসার্ধ নিয়ে BC এর একই পাশে দুটি বৃত্তচাপ আঁকি। বৃত্তচাপ দুটি পরস্পর A বিন্দুতে ছেদ করে।

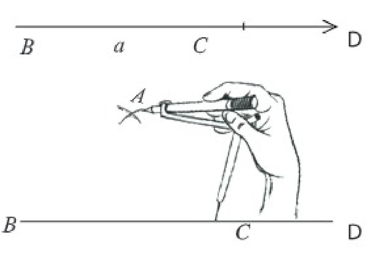
(৩) A, B এবং A, C যোগ করি। তাহলে ∆ABC-ই উদ্দিষ্ট ত্রিভুজ।

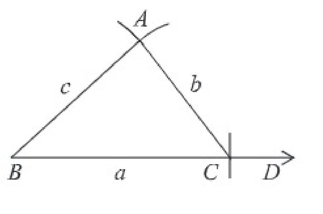
প্রমাণ: অঙ্কনানুসারে, ∆ABC এ BC = a, AC = b এবং AB = c.

∴ ∆ABC প্রদত্ত বাহুযুক্ত ত্রিভুজ।

কাজ ১। 8 সে.মি., 5 সে.মি. ও 6 সে.মি দৈর্ঘ্যের তিনটি বাহুবিশিষ্ট একটি ত্রিভুজ আঁক। ২। 12 সে.মি., 5 সে.মি. ও 6 সে.মি দৈর্ঘ্যের তিনটি বাহুবিশিষ্ট একটি ত্রিভুজ অঙ্কনের চেষ্টা কর। তোমার চেষ্টা সফল হয়েছে কি?

মন্তব্য: ত্রিভুজের দুই বাহুর সমষ্টি এর তৃতীয় বাহু অপেক্ষা বৃহত্তর। তাই প্রদত্ত বাহুগুলো এমন হতে হবে যে, যেকোনো দুটির দৈর্ঘ্যের সমষ্টি তৃতীয়টির দৈর্ঘ্য অপেক্ষা বৃহত্তর হয়। তাহলেই ত্রিভুজটি আঁকা সম্ভব হবে।

সম্পাদ্য ২

কোনো ত্রিভুজের দুইটি বাহু ও এদের অন্তর্ভুক্ত কোণ দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

মনে করি, একটি ত্রিভুজের দুইটি বাহু a ও b এবং তাদের অন্তর্ভুক্ত কোণ ∠X দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কন:

(১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC নিই।

(২) BC রেখাংশর C বিন্দুতে প্রদত্ত ∠ x এর সমান ∠BCE আঁকি।

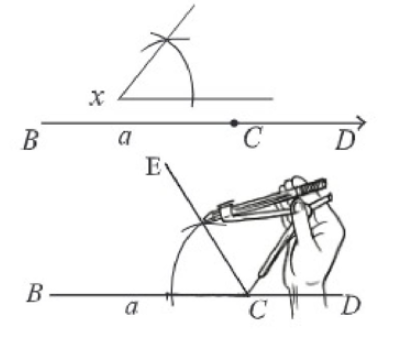
(৩) CE রেখাংশ থেকে b এর সমান করে CA নিই। A, B যোগ করি। তাহলে $∆$ABC ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ: অঙ্কন অনুসারে,

∆ABC-এ BC = a, CA = b এবং ∠ ACB = ∠ x.

∴ ∆ABC ই নির্দিষ্ট ত্রিভুজ।

সম্পাদ্য ৩

কোনো ত্রিভুজের একটি বাহু ও এর সংলগ্ন দুটি কোণ দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

মনে করি, একটি ত্রিভুজের একটি বাহু ৫ এবং এর সংলগ্ন দুটি কোণ ∠ x ও ∠ y দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

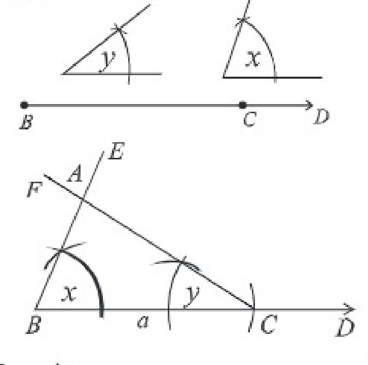
অঙ্কন:

(১) যেকোনো রশ্মি BD থেকে ৫ এর সমান করে BC নিই।

(২) BC রেখাংশের B ও C বিন্দুতে যথাক্রমে ∠ x এবং ∠y এর সমান করে ∠ CBE এবং ∠ BCF আঁকি। BE ও CF পরস্পর A বিন্দুতে ছেদ করে।

তাহলে $∆$ABC ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ: অঙ্কন অনুসারে,

$∆$ABC - 4BC = a ∠ ABC = ∠ x এবং ∠ ACB = ∠ y.

∴ $∆$ABC ই নির্দিষ্ট ত্রিভুজ।

মন্তব্য: ত্রিভুজের তিন কোণের সমষ্টি দুই সমকোণের সমান, তাই প্রদত্ত কোণ দুটি এমন হতে হবে যেন এদের সমষ্টি দুই সমকোণ অপেক্ষা ছোটো হয়। এই শর্ত পালন করা না হলে কোনো ত্রিভুজ আঁকা সম্ভব হবে না।

সম্পাদ্য ৪

কোনো ত্রিভুজের দুইটি কোণ এবং এদের একটির বিপরীত বাহু দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।
মনে করি, একটি ত্রিভুজের দুটি কোণ ∠A ও B এবং ∠A এর বিপরীত বাহু a দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

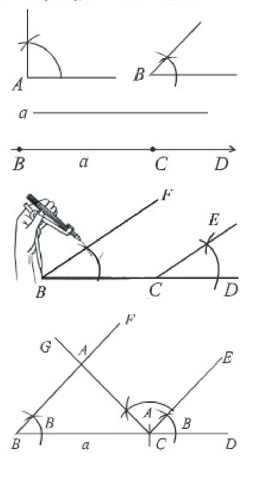
অঙ্কন:

(১) যেকোনো রশ্মি BD থেকে a এর সমান করে BC নিই।

(২) BC রেখাংশের B ও C বিন্দুতে ∠B এর সমান করে ∠CBF ও ∠DCE আঁকি।

(৩) এখন CE রেখার C বিন্দুতে ∠A এর সমান করে ∠ECG আঁকি। CG ও BF রেখা A বিন্দুতে ছেদ করে।

∴ ত্রিভুজ ABC ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ: অঙ্কনানুসারে, ∠ABC = ∠ECD. এই কোণ দুটি অনুরূপ বলে BF || CE বা BA || CE এখন BA || CE এবং AC এদের ছেদক।

∴ ∠BAC=একান্তর ∠ACE = ∠A.

এখন ∆ABC এ ∠BAC = ∠A, ∠ABC = ∠B এবং BC = a. সুতরাং, ABC ত্রিভুজটি শর্তমতে অঙ্কিত হলো।

সম্পাদ্য ৫

কোনো ত্রিভুজের দুটি বাহু এবং এদের একটির বিপরীত কোণ দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

মনে করি, একটি ত্রিভুজের দুটি বাহু a ও b এবং b বাহুর বিপরীত কোণ ∠B দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কন:

(১) যেকোনো রশ্মি BD আঁকি।

(২) B বিন্দুতে প্রদত্ত ∠B এর সমান করে ∠DBE আঁকি। BE রেখা থেকে c এর সমান করে BA নিই।

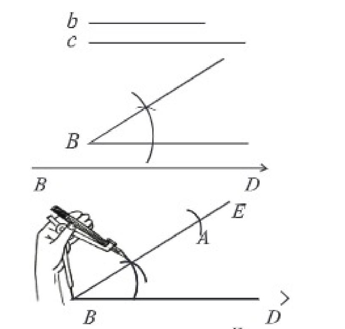
(৩) এখন এ বিন্দুকে কেন্দ্র করে ৮ এর দৈর্ঘ্যের সমান ব্যাসার্ধ নিয়ে BD রেখার উপর একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি BD রেখাকে Cও C' বিন্দুতে ছেদ করে। A, C এবং A.C" যোগ করি। তাহলে ∆ABC এবং ∆ABC'-উভয় ত্রিভুজ প্রদত্ত শর্ত পূরণ করে অঙ্কিত।

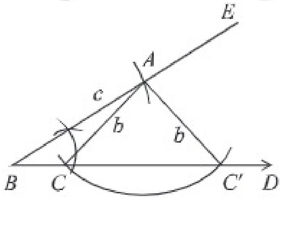
প্রমাণ: অঙ্কনানুসারে, ∆ABC এ BA = c, AC = b এবং ∠ABC = ∠B

আবার, ∆ABC" - এ BA = c, AC' = b এবং ∠ABC' = ∠B

দেখা যায়, ∆ABC এবং ∆ABC" উভয়ই প্রদত্ত শর্তসমূহ পূরণ করে।

তাহলে ∆ABC বা ∆ABC'-ই উদ্দিষ্ট ত্রিভুজ।

সম্পাদ্য ৬

কোনো সমকোণী ত্রিভুজের অতিভুজ ও অপর একটি বাহু দেওয়া আছে, ত্রিভুজটি আঁকতে হবে।

মনে করি, একটি সমকোণী ত্রিভুজের অতিভুজ a ও অপর এক বাহু b দেওয়া আছে। ত্রিভুজটি আঁকতে হবে।

অঙ্কন:

(১) যেকোনো রশ্মি BD থেকে b এর সমান করে BC নিই।

(২) BC রেখার B বিন্দুতে BE লম্ব আঁকি।

(৩) C কে কেন্দ্র করে a এর সমান ব্যাসার্ধ নিয়ে BE রেখার উপর একটি বৃত্তচাপ আঁকি, যেন এটি BE-কে A বিন্দুতে ছেদ করে। A ও C যোগ করি। তাহলে ∆ABC-ই উদ্দিষ্ট ত্রিভুজ।

প্রমাণ: অঙ্কনানুসারে, AC = a, BC = b এবং ∠ABC = এক সমকোণ।

∴ ∆ABC-ই নির্ণেয় ত্রিভুজ।